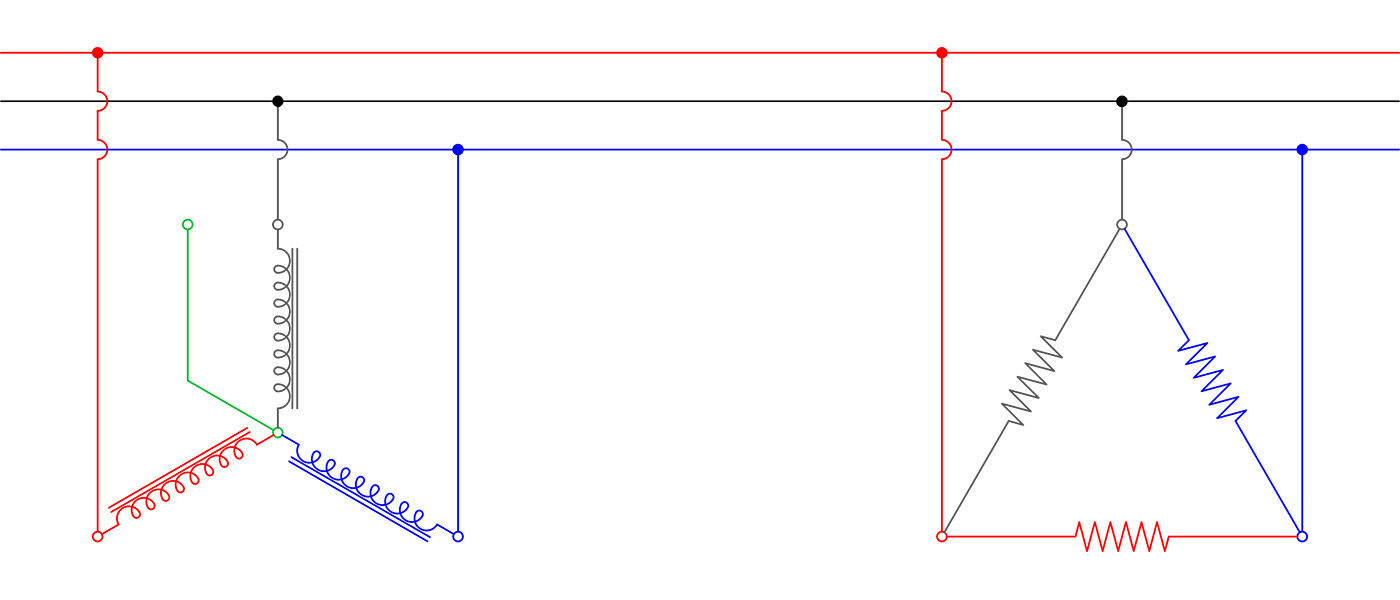
A three-phase system has two loads with the following information:

• A wye-connected motor load has a phase voltage of 277.2 V and a phase current of 25 A. This motor is operating with a 0.866 power factor.
• A heating load is delta-connected with 11 ohms of resistance in each phase.

1. Since the question has given us V_PHASE for the Wye load, we can use this to determine our line voltage for both loads.

   In a Wye system V_LINE = V_PHASE × 1.732 (√3)

   V_{LINE (WYE)} = 277.2 V × 1.732
   V_{LINE (WYE)} = 480.124 V

   We also know that the delta connected load is connected in parallel to the wye-connected load. This tells us that the line voltage will be the same in both loads.

   V_{LINE (DELTA)} = V_{LINE (WYE)}
   V_{LINE (DELTA)} = 480.124 V

2. Next we can solve for the phase current in the delta.

   Ohm's law states that Current (I) = Voltage (V) ÷ Resistance (R), or I = V÷R

   We know that we have 11 Ω resistance is each phase of the delta so we need to get the phase voltage.

   In a delta V_PHASE = V_LINE so V_PHASE = 480.124 V

   Now we can calculate the phase current.

   I_{PHASE (DELTA)} = 480.124 V ÷ 11 Ω
   I_{PHASE (DELTA)} = 43.64768035 A

3. The last piece of information we need to find is the total line current for the system.

   Since the wye-connected motor load is operating at a lagging power factor our two loads are not in phase with one another.

   This means we need to phasorically add the line current of the wye to the current of the delta.

   In a wye configuration, I_LINE = I_PHASE, so I_{LINE (WYE)} = 25 A

   We also need to know the power factor angle for this load.

   Pf∠ = cos^-1(pf)
   Pf∠ = cos^-1(0.866)
   Pf∠ = 30.00291093°

   We can now say that I_{LINE (WYE)} = 25 A @ 30.00291093°

   Next we need to know the line current for the delta load.

   In step 2 we calculated the delta phase current. In a delta system I_LINE = I_PHASE × 1.732 (√3)

   I_{LINE (DELTA)} = I_{PHASE (DELTA)} × 1.732 (√3)
   I_{LINE (DELTA)} = 43.64768035 A × 1.732 (√3)
   I_{LINE (DELTA)} = 75.6 A

   Since this is a purely resistive load we know that the power factor is 1 (unity) so we have 75.6 A @ 0°

   We can now add our two line currents phasorically (using a horizontal / vertical chart) to calculate the total line current.

   Load	Horizontal	Vertical
   ILINE (WYE) = 25 A @ 30.00291093°	cos(30.00291093) × 25.0 = 21.65	sin(30.00291093) × 25.0 = 12.50109995
   ILINE (DELTA) = 75.6 A @ 0°	cos(0) × 75.6 = 75.60	sin(0) × 75.6 = 0.00000000
   Totals	97.25	12.50109995

   Now that we have the horizontal and vertical totals, we can use Pythagorean theorem to calculate the total Line Current.

   I_{LINE (TOTAL)}² = Horizontal Total² + Vertical Total²
   I_{LINE (TOTAL)}² = 97.25² + 12.50109995²
   I_{LINE (TOTAL)}² = 9,613.84
   I_{LINE (TOTAL)} = √9,613.84
   I_{LINE (TOTAL)} = 98.05019123